Overview

Polygenic or epistatic effect analysis can provide a sound biological explanation of GxG. Dr. Shizhong Xu (UC-Riverside) has proposed a polygenic LMMs, which can estimate the non-additive genetic effects, such as dominance, and epistasis. Based on this LMMs, we have developed a pipeline entitled as PEPIS Before estimating the epistatic effects, the calculation of epistatic kinship matrix together with the conventional kinship matrix is the first step. The epistatic effect is defined as the genotypic marker pairs, which cause the epistatic effect kinship matrix calculation is very time-consuming. To speed up, PEPIS adopted a parallel computing architecture by deploying several hundreds~ one thousand CPU nodes . PEPIS with this architecture really work very fast but its cost is also very huge.

In the recent years, GPU(Graphics Processing Units) with multiple hardware processor cores has become a standard HPC (High Performance Computing) solution system for large scale computing. GPU favors to large scale matrix operations, and also do not occupy too much valuable CPU resource.

We have analyzed the math principle and the complexity of epistatic kinship matrix, then we have successfully developed this GPU empowered pipeline for epistatic effect kinship matrix calculating: KMC2D , which can easily realize several hundreds of times of speeding up, when compared with the golden single processing.

Rationale

Compared with genotypic marker's direct effect, epistatic effect essentially can be mathematically defined as the marker pairs. Suppose there are m markers, the marker pairs correspond to the epistatic effect can amount to C(m,2)=m(m-1)/2 . If we consider the marker pair as a synthesis marker, then, the routine to calculate conventional kinship matrix can be completely apply to the epistatic kinship matrix. This means that the complexity of epistatic effect kinship matrix is O(m^2) instead of the original complexity O(m). Additionally, the kinship matrix is of linearity, which can be acquired by summing a bunch of sub-kinship matrix, and each sub-kinship matrix is calculated by a block of successive markers. Fig.1 depict the math rationale to generate the marker pairs and partition all the marker pairs into successive blocks for sub kinship matrix calculating.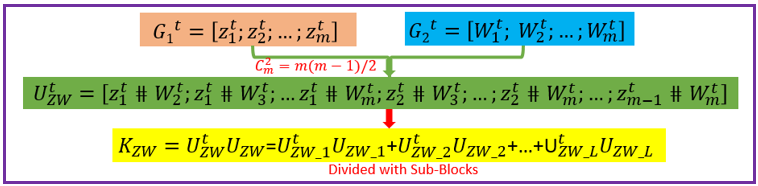

Fig. 1 The illustration of math principle to generate the marker pairs and partition all the marker pairs into successive blocks for sub kinship matrix calculating

GPU based parallel computing favors to compute large scale matrix operations. Ideally, each matrix entry operation can be implemented by one thread corresponds to one GPU core. All the GPU program include two parts: one as the host part running on CPU , and the other part as kernel codes running on the slavery device-GPU cores. The GPU kernel codes are functionally implemented by parallelization and distinguished by the specific primitive _global_. We analyzed the mathematical principle and the matrix operation procedure to calculate kinship matrix, and coded 4 GPU core paralleling kernel functions including transpose of matrix, multiplication of two matrix, sum of two matrix, and the normalization of the sum kinship matrix. Fig.2 depict the GPU empowered parallel pipeline architecture for epistatic kinship matrix calculating through partitioning marker pairs into successive blocks, then calculating sub kinship matrix and merging into a whole.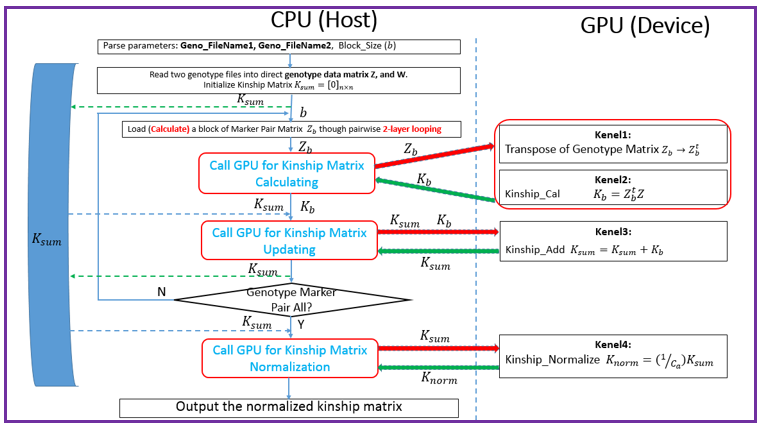

Fig.2 GPU empowered parallel pipeline architecture for epistatic kinship matrix calculating

Representative Application of KMC2D

Equipped with GPU parallel computing, KMC2D can calculate the epistatic (2D) kinship matrix for the given genotype data. The polygenic LMMs need two kinds of genotype data: one is for additive effect (Z_matrix) and the other is for dominance effect(W_matrix), therefore, there should have at least three kinds of representative applications.

1.)Upload the additive effect Z_Matrix for both the 1st and 2nd genotype matrix file, then you will get the epistatic kinship matrix for additive-additive. Fig.3 provide the user-interface snapshot for epistatic additive-additive kinship matrix calculating.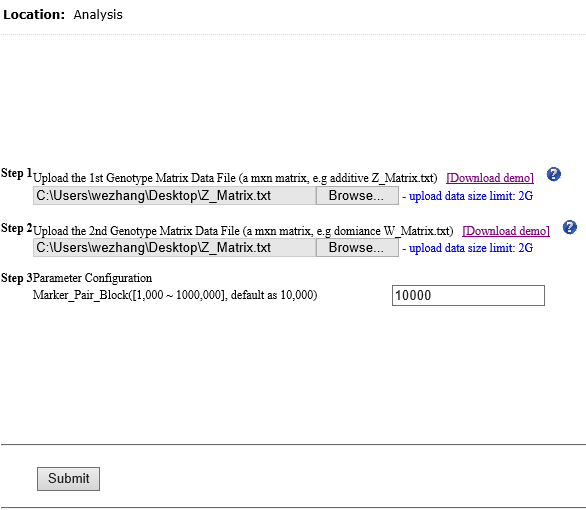

Fig. 3 The interface for uploading the additive Z_Matrix as both the 1st and 2nd genotype matrix files

2.)Upload the additive effect Z_Matrix and dominance effect W_Matrix for the 1st and 2nd genotype matrix files, then you will get the epistatic kinship matrix for additive-dominance. Fig.4 provide the user-interface snapshot of uploading files for epistatic additive-dominance kinship matrix calculating.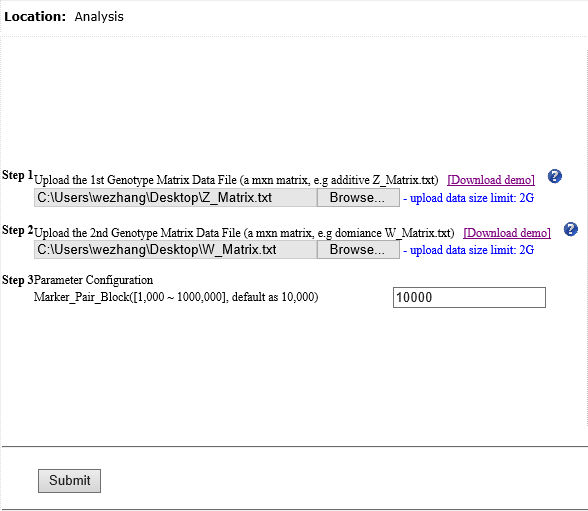

Fig. 4 The interface for uploading the additive Z_Matrix and dominance W_Matrix as the 1st and 2nd genotype matrix files

3.)Upload the dominance effect W_Matrix for both the 1st and 2nd genotype matrix files, then you will get the epistatic kinship matrix for dominance-dominance. Fig.5 provide the user-interface snapshot of uploading files for epistatic dominance-dominance kinship matrix calculating.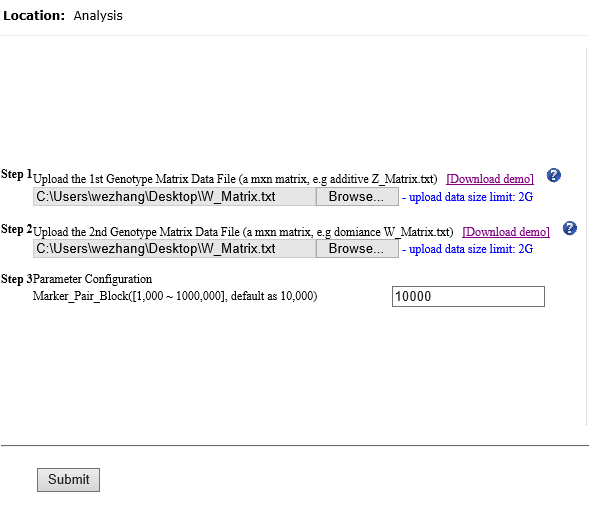

Fig. 5 The interface for uploading the additive Z_Matrix and dominance W_Matrix as the 1st and 2nd genotype matrix files

If you submit other omics (such as transcriptomics, metabolomics data) marker matrix, you also can get the corresponding 2D kinship matrix. At this application, the marker matrix data are not limited to binary format and mostly as float format.

Reference:

1. Xu, S., "Mapping Quantitative Trait Loci by Controlling Polygenic Background Effects". 2013, Genetics, 195(4):p.1709-23

2. Zhang W., Dai X., Wang Q, Xu S., Zhao P.X., "PEPIS: A Pipeline for Estimating Epistatic Effects in Quantitative Trait Locus Mapping and Genome-Wide Association Studies", 2016, PLoS Comput Biol, 12(5).

3. Cecilia J. M. , Garc´ıa J. M. , and Ujaldon M., “The GPU on the Matrix-Matrix Multiply: Performance Study and Contributions”, in Parallel Computing: From Multicores and GPU’s to Petascale, B. Chapman et al., 2010, Advances in Parallel Computing, vol. 19, pp. 331-340.

4. Dobravec T., Bulic P., "Comparing CPU and GPU Implementations of a Simple Matrix Multiplication Algorithm", 2017, IJCEE, vol 9, 430-438.